Sujet :
Les parenthèses
Description :
Dans une opération, les parenthèses indiquent qu’il faut calculer une partie avant une autre.
Pré-Requis :
Savoir calculer avec les 4 opérations de base : + – x /
Leçon :
Le symbole « parenthèses » ( )
Une parenthèse est composée de deux signes typographiques – le signe « ( » et le signe « ) » – entre lesquels on place quelque chose.
Pour commencer, mettons nos « lunettes à parenthèse ». Pourquoi ? Parce que les lunettes comme les parenthèses marchent par deux et ne peuvent jamais se retrouver seules.
Qui a eu cette idée ? Et à quoi cela sert-il ?
C’est M. Tartaglia qui a utilisé le premier les parenthèses en mathématiques, au XVIè siècle.

En mathématiques, dans un calcul, il s’agit d’indiquer que l’on doit calculer une partie avant une autre.
Un premier exemple :
10 – 3 + 2 ne va pas donner le même résultat que 10 – (3 + 2)
10 – 3 + 2 c’est égal à… 9
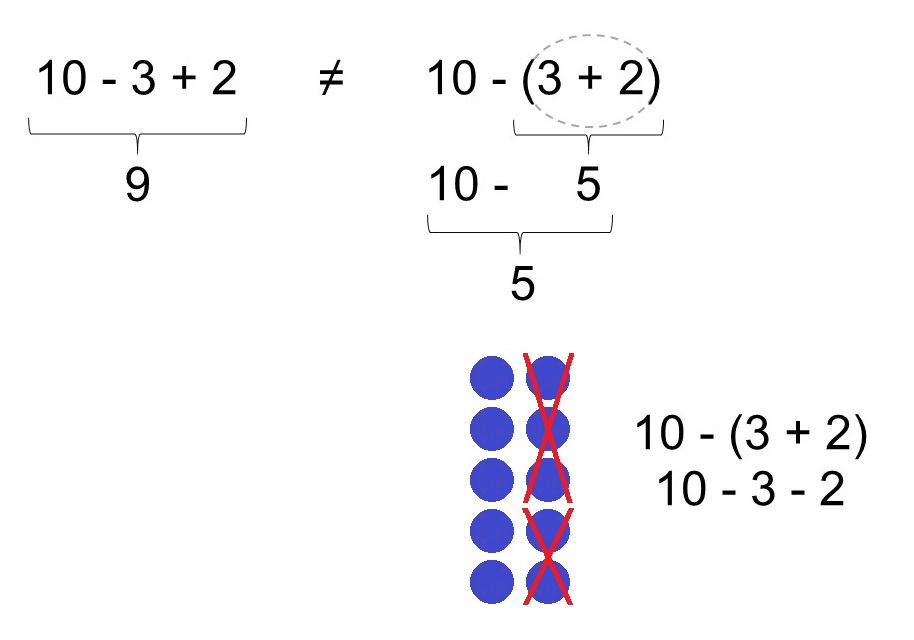
Quand on ajoute une parenthèse, cela indique qu’il faut d’abord calculer ce qu’il y a entre les signes ( ) et donc ici (3 + 2). Et seulement ensuite on calcule 10 – 5 = 5.
On voit donc que, dans 10 – (3 + 2), on veut ôter à la fois 3 et 2 à 10.
Une énigme à résoudre :
J’ai 10 pommes. J’en prends 3 pour faire une tarte, et 2 pour faire une compote. Combien m’en reste-t-il ?
10 pommes, desquelles je soustrais (donc je mets le signe » – « ) 3 pommes pour la tarte et 2 pommes pour la compote. Cela donne 10 – (3 + 2) parce que j’ai mis entre parenthèses tout ce que je vais prendre, donc ici « 3 + 2 ».
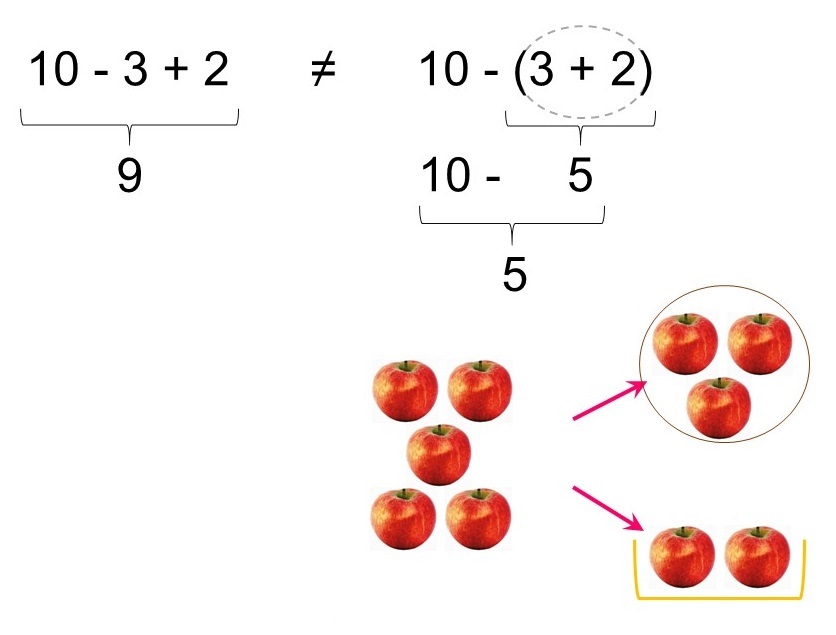
Remarque : soustraire 3 et 2 revient à soustraire 3 puis à soustraire 2.
Donc 10 – (3 + 2) = 10 – 3 – 2.
Qu’on enlève 5 d’un coup, ou qu’on enlève 3, puis 2, c’est pareil.
Où placer les parenthèses ?
Dans ce calcul, où doit-on placer les parenthèses ?
4 – 9 – 6 = 1.
On ne peut pas les placer au début, car on ne sait pas calculer 4-9, mais si on les place à la fin, on obtient bien 4 – (9 – 6) = 4 – 3 = 1.
Repères :
Dès que tu vois des parenthèses dans un calcul.
Dès que tu dois retirer plusieurs choses en même temps.
Entraîne-toi
L’enjeu est de réussir à toujours penser à :
– chausser ses lunettes à parenthèses pour détecter qu’il y a des parenthèses, comme dans la vidéo ![]()
– avoir le réflexe de commencer par calculer ce qu’il y a dedans.

![]()
![]()
![]()
