Sujet :
Fractions & Proportions
Description :
Les pourcentages sont un cas particulier de proportionnalité, très utilisé dans tous les domaines pour parler de sous-groupes (« 30% de la population sont… ») ou de variations (« -2% d’accidents par rapport à l’année dernière… »)
Leçon :
Prérequis : la leçon « Fractions et proportions »
Le pourcentage est un cas particulier de proportionnalité où l’on donne une proportion pour 100 éléments.
« Pour cent » est tellement utilisé que c’est devenu un nom commun : le « pourcent », et son symbole mathématique est « % ».
Il fonctionne comme n’importe quelle autre proportionnalité et est très utilisé pour parler de sous-groupes ou de variations.
Pourcentages représentant des sous-groupes
Exemple : en Grèce, 15 % de la population a moins de 14 ans.
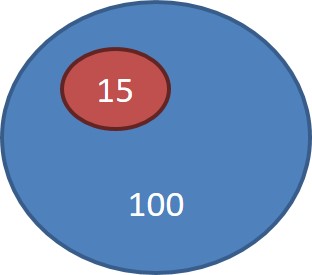
Cela veut dire que pour chaque groupe de 100 personnes, on trouve en moyenne 15 enfants (de moins de 14 ans).
Sachant qu’il y a 11 millions de personnes en Grèce, on peut trouver le nombre d’enfants en utilisant la règle de trois habituelle :
| Nombre de personnes | Nombre d’enfants |
| 100 | 15 |
| 1 | 15/100 |
| 11 millions | 11 000 000 x 15/100 enfants = 1 650 000 |
Pourcentages représentant des variations
Exemple : le magasin fait des soldes à « 20% de remise sur tous les articles »
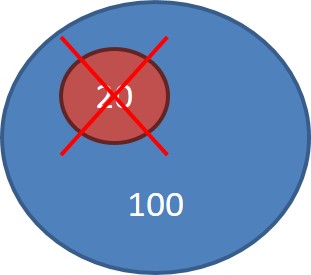
On utilise toujours la règle de trois pour trouver combien il faudra retirer en prix initial pour trouver le prix final.
| Prix de l’article | Réduction | Prix final |
| 100 | 20 | 80 |
| 1 | 20/100 | 1 – 20/100 |
| 80 | 80 x 20/100 = 16 | 80 – 16 = 64 |
Pourcentages repères à retenir
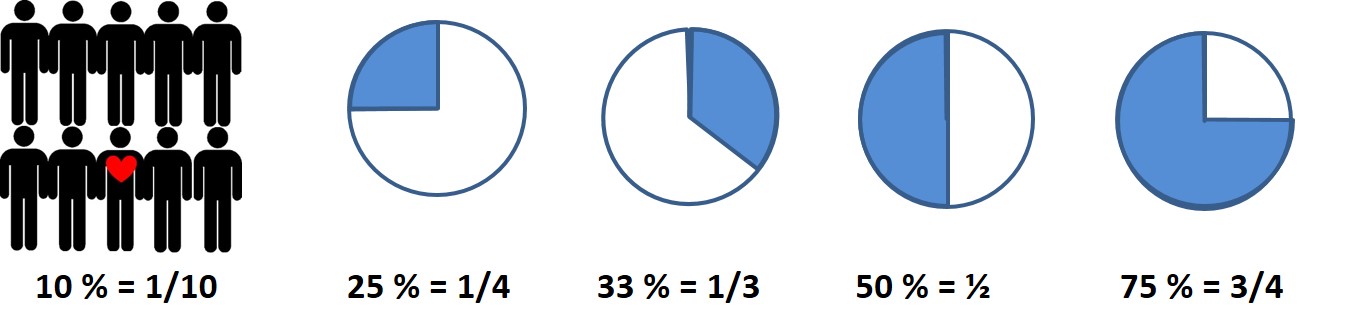
Repères :
Dès que je dois parler de proportions, j’essaie de les transformer en pourcentages pour que cela soit plus facile de se les représenter. Les gens comprendront bien mieux de quoi je parle !
