Sujet :
Division et fractions
Description :
Les approximations sont pratiques pour se donner une idée du résultat d’un calcul. Ici on travaille sur l’approximation des fractions.
Leçon :
Prérequis : La leçon « Fractions : entier + fraction inférieure à 1 » et les leçons sur les encadrements
On sait déjà que encadrer par 2 entiers consécutifs, c’est encadrer par 2 entiers qui se suivent.
On a aussi vu comment trouver une valeur approchée d’une fraction, on la décomposant en un entier et une fraction inférieur à 1, par exemple 7/4 = 1 + ¾. Ici 1 est la valeur approchée par défaut (inférieure, juste en-dessous).
On sait donc écrire 1 < 7/4
et pour finir l’encadrement, je n’ai plus qu’à donner le nombre juste après 1, donc 2 :
1 < 7/4 < 2
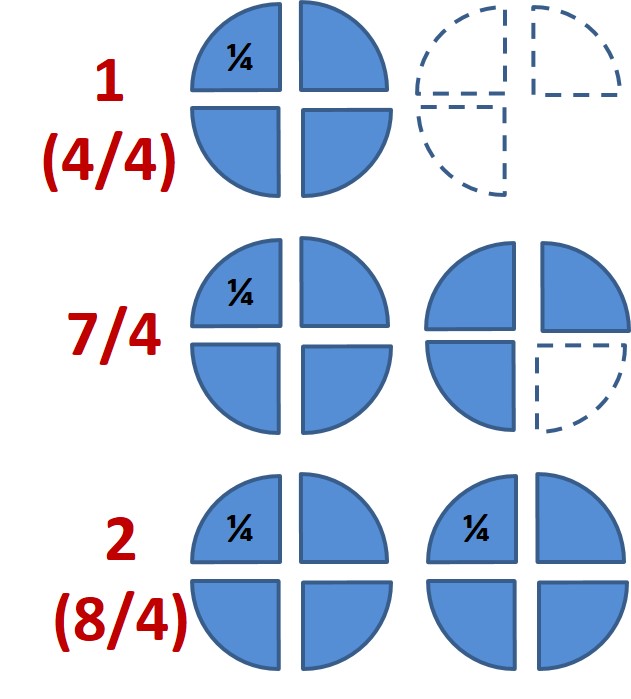
On voit que :
– la valeur approchée inférieure (par défaut) revient à ignorer les fragments d’unité (les décimales),
– la valeur approchée supérieure (par excès) revient à ajouter des fragments pour compléter l’entier qui n’était pas complet.
NB : une fois qu’on a trouvé l’entier le plus proche, il est facile d’encadrer à la dizaine près, donc entre 2 dizaines consécutives, ou à la centaine près, ou à tout ce qu’on veut près.
Par exemple si on veut encadrer 118/5, on va trouver que c’est 23 + 3/5, donc on peut écrire :
– à l’unité près : 23 < 118/5 < 24
– à la dizaine près : 20 < 118/5 < 30
– à la centaine près : 0 < 118/5 < 100
Repères :
Chaque fois que je veux estimer, évaluer, approcher une fraction.
