Sujet :
Fractions & Proportions
Description :
Cas plus complexes de comparaisons de fractions.
Leçon :
Prérequis : les leçons « Fractions : entier + fraction inférieure à 1 », « Fractions équivalentes et simplification » et « Fractions et proportions ».
En plus de la leçon précédente « Comparer les fractions : même numérateur ou même dénominateur » tu connais encore d’autres astuces pour réussir à comparer des fractions, pense à les utiliser !
Simplifier pour retrouver le même dénominateur (quand c’est possible)
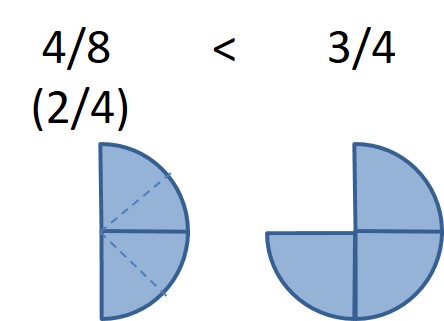
Exemple : pour comparer 4/8 et 3/4, je peux remarquer que 4/8 est équivalente à 2/4.
Je n’ai donc plus qu’à comparer 2/4 et 3/4, ce que je sais déjà faire.
Approcher les fractions
Si toutes les astuces précédentes ne fonctionnent pas, je peux décomposer les fractions sous forme « entier + petite fraction inférieure à 1 ».
Exemple : pour comparer 23/6 et 13/5, j’écris que
23/6 = 18/6 + 5/6 = 3 + 5/6 et
13/5 = 10/5 + 3/5 = 2 + 3/5
Comme on sait que les petites fractions restantes sont inférieures à 1, alors 2 + 3/5 ne pourra jamais dépasser 3, donc on trouve forcément 23/6 > 13/5
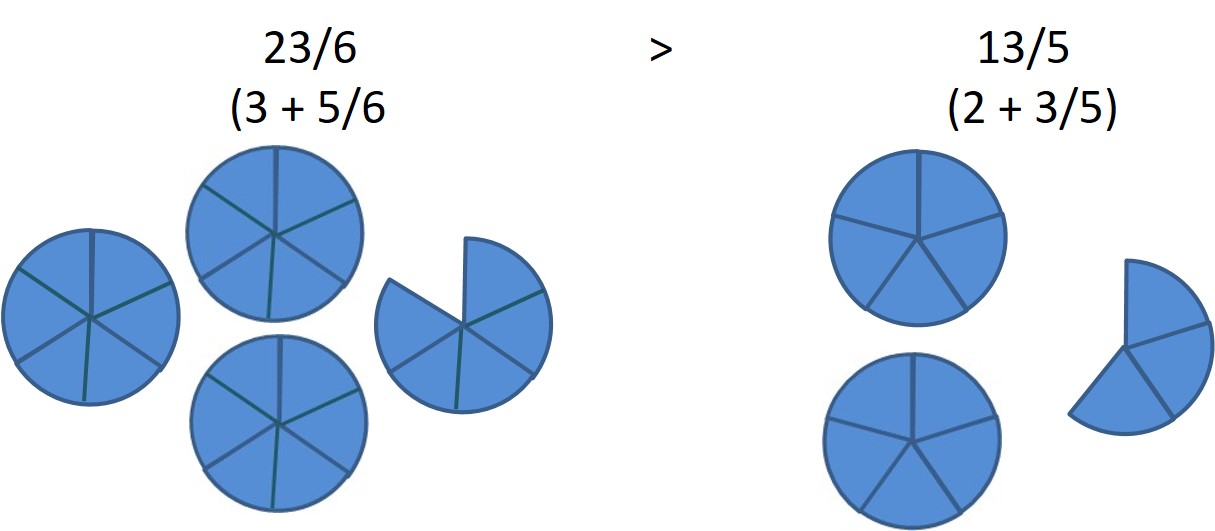
Si aucune autre astuce n’est possible !
Tu peux toujours commencer à poser les divisions, et voir dès que les décimales deviennent différentes.
Exemple : comparer 8/6 et 10/7
Si on les décompose, on trouve 1 + 2/6 et 1 + 3/7, donc à nouveau on ne sait pas trop lequel est le plus grand. Alors tant pis, on commence à poser les divisions et on voit alors dès la 1èredécimale que
8/6 = 1,3…
10/7 = 1,4…
donc finalement :
10/7 > 8/6
(1,4… > 1,3…)
Pas la peine de calculer les autres décimales !
Au final, tu peux donc utiliser toutes ces astuces :

Repères :
Chaque fois que je dois comparer ou manipuler des fractions en général, je vois dans ma tête tout ce que je sais faire avec les fractions, et j’utilise ce qui est le plus pratique.
