Sujet :
Division
Description :
Comme pour les autres opérations, poser une division permet de faire ce calcul, généralement pour des grands nombres, qu’on ne saurait pas faire de tête.
Leçon :
Prérequis : les leçons « Division : se servir des tables de multiplication » et « Le système décimal/base 10 – Les centaines »
Tu te souviens que l’on peut voir la division comme : partager une quantité en plusieurs paquets égaux, et voir quelle quantité il y a dans chaque paquet.
Pour les grands nombres, on va devoir partager non seulement les unités, mais aussi les dizaines et les centaines.
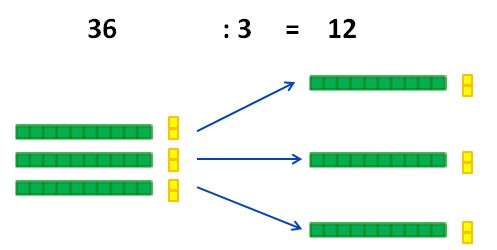
Par exemple calculons 36 : 3. On répartit en 3 paquets égaux, donc chaque paquet aura 1 dizaine et 2 unités, donc 36 : 3 = 12.
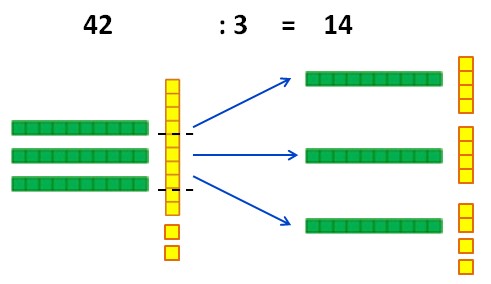
Autre exemple : 42 ÷ 3. Ici aussi on va avoir 1 dizaine dans chaque paquet, mais il restera une dizaine, donc on utilise toujours la même astuce : on casse la dizaine en 10 unités, ce qui nous fait au total 12 unités à partager. On a alors 4 unités par paquet. Au total chaque paquet à 1 dizaine et 4 unités, donc 42 : 3 = 14.
Dernier exemple : 43 ÷ 3. C’est exactement pareil que 42 ÷ 3, mais il y a une unité de plus, qu’on ne va pas savoir partager. On dira alors « 43 ÷ 3 = 14 reste 1 » car il reste une unité qu’on ne peut pas diviser.
Je te rappelle que pour trouver la division 13 : 3, tu dois te demander 3 x combien = 13. Comme 3 x 4 = 12 (pas assez) et 3 x 5 = 15 (trop), cela veut dire que tu peux diviser en 4 mais qu’il restera 1 unité que tu ne pourras pas diviser.
Pour poser la division, il ne reste plus qu’à faire pareil mais en l’écrivant.
Pour la division, on se sert d’un tableau différent de celui utilisé pour les autres opérations.
Cette nouvelle présentation permet de bien voir tout ce qu’il reste à répartir à chaque étape :
– On commence par diviser les centaines et on écrit combien il y en a dans chaque paquet.
– S’il reste des centaines qu’on ne peut pas répartir, on les transforme en dizaines et on écrit combien de dizaines au total on va devoir partager. (Pour s’aider, on peut écrire le nombre de centaines qu’on a réparties pour calculer combien il en reste.)
– Puis on fait la division des dizaines et on écrit combien il y en a dans chaque paquet.
– S’il reste des dizaines qu’on ne peut pas répartir, on les transforme en unités et on écrit combien d’unités au total on va devoir diviser. (Pour s’aider, on peut écrire le nombre de dizaines qu’on a réparties pour calculer combien il en reste.)
– Puis on fait la division des unités et on écrit combien il y en a dans chaque paquet.
S’il reste des unités qu’on ne peut pas répartir, on les écrit pour montrer qu’il en reste. (Pour s’aider, on peut écrire le nombre d’unités qu’on a réparties pour calculer combien il en reste.)
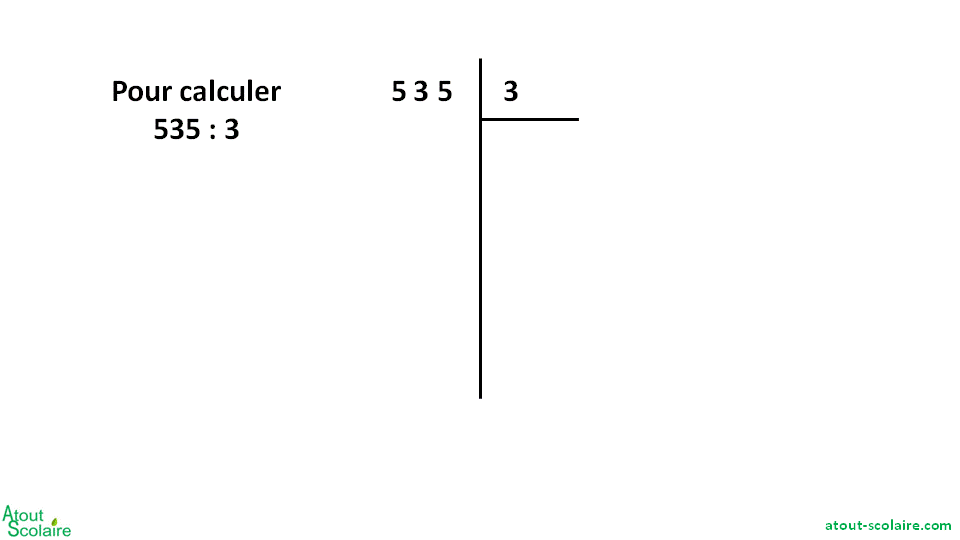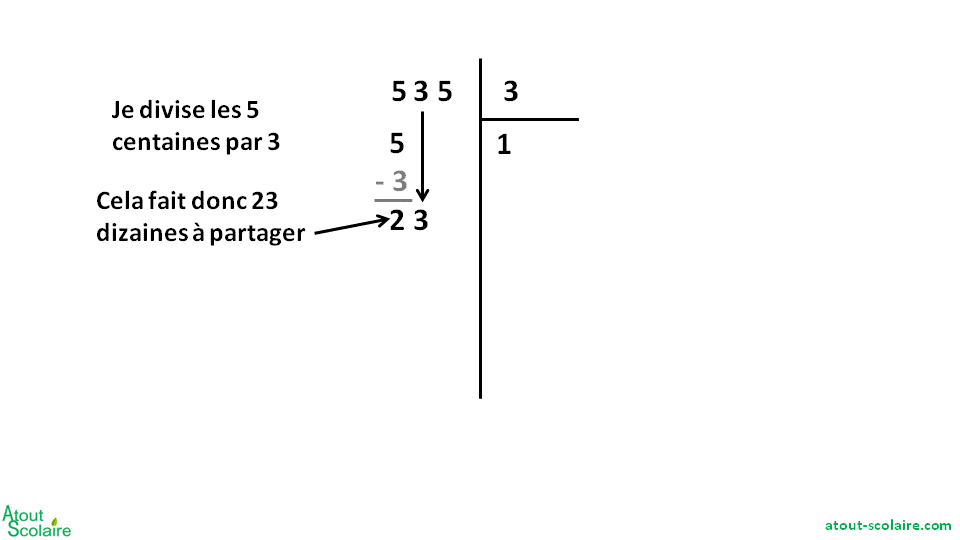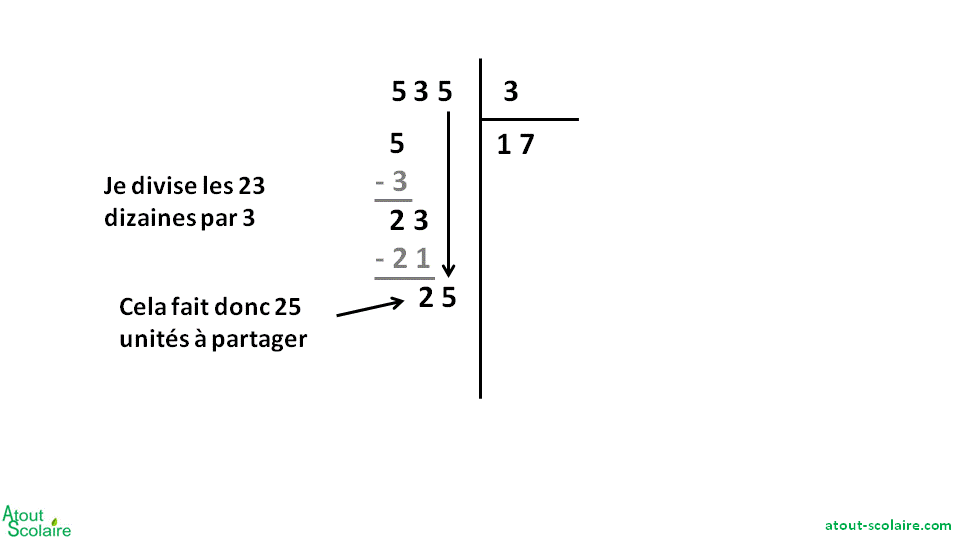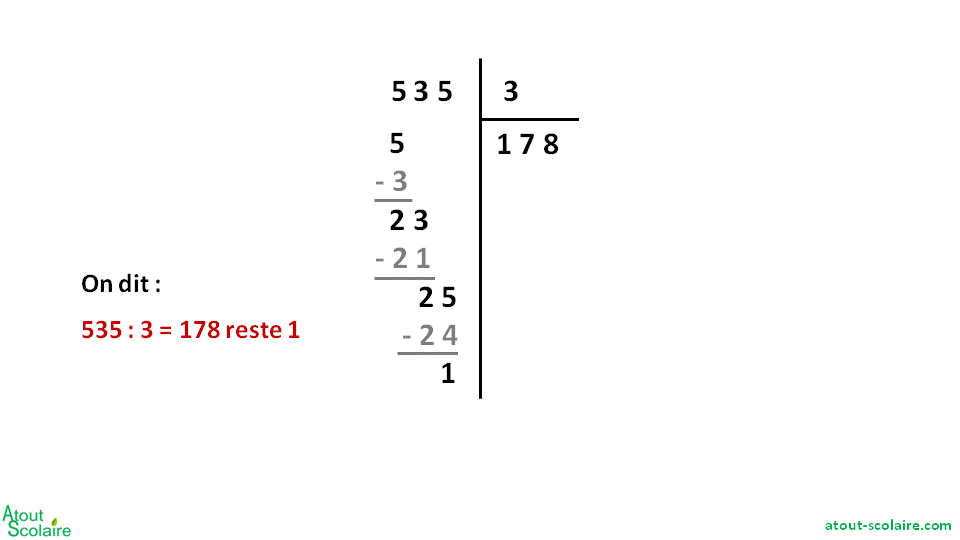
Repères :
Chaque fois que je dois calculer une division que je ne peux pas faire de tête.
Entraîne-toi :
Tu trouveras des exercices à faire en cliquant ici pour te rendre sur le site Revisez.eu.
![]()
![]()
![]()
