Sujet :
Proportions / Conversions
Description :
La proportionnalité est le fait de conserver le rapport, les proportions qu’il y a entre deux quantités. C’est la base des calculs de conversion qui correspondent à de nombreux.
Leçon :
La proportionnalité est le fait de conserver le rapport, les proportions qu’il y a entre deux quantités. C’est la base des calculs de conversion qui correspondent à de nombreux cas rencontrés au quotidien (distance, durée, échelle, pourcentages). Elle permet également de réussir ses recettes et de payer le prix juste 😉
Prérequis : La leçon « Comprendre la multiplication » et les tables de multiplication
Proportion
Une proportion, c’est le rapport qu’il y a entre 2 quantités, c’est-à-dire, combien vaut une quantité par rapport à une autre.
Exemple : si je dois utiliser 2 pommes pour cuisiner une tarte pour 4 personnes, on dit que la proportion est de 2 pommes pour 4 personnes.
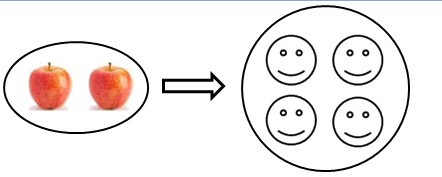
Proportionnalité
C’est le fait de conserver les proportions.
Exemple : si je veux cuisiner une tarte pour 12 personnes, je dois garder la même proportion de pommes pour que la tarte soit réussie. Comme j’en veux pour le triple de personnes, il faut aussi que j’utilise le triple de pommes, donc 6.
On pouvait aussi dire que si je possède 6 pommes, alors je peux cuisiner 3 fois plus qu’avec 2 pommes, donc pour 3×4=12 personnes.
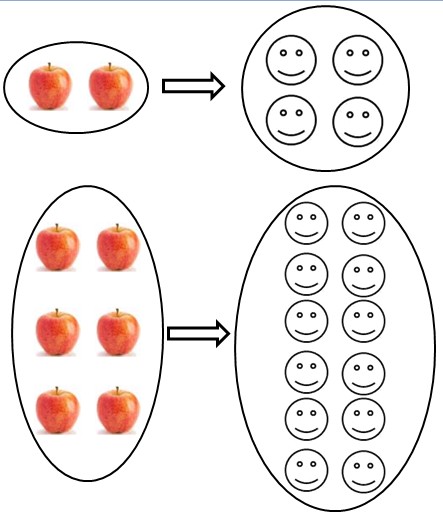
Tableau de proportionnalité
Pour s’y retrouver plus facilement, on peut écrire dans un tableau les quantités pour différents nombres de parts.
Comme on respecte toujours les mêmes proportions, on appelle cela un tableau de proportionnalité.
Exemple :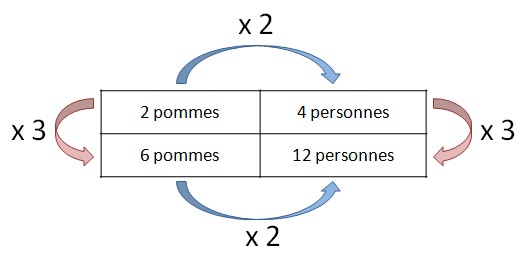
On voit que pour passer d’une ligne à une autre, on multiplie toute la ligne par une même quantité. Et pour passer d’une colonne à une autre, on multiplie toute la colonne par une même quantité aussi.
Du coup, c’est facile de savoir si on s’est trompé : un élément est faux s’il n’est pas multiplié pareil que les autres de la même ligne ou de la même colonne.
Exemple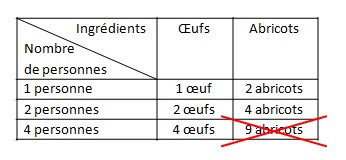
Ici nous avons 2 manières de savoir que « 9 abricots » est faux :
– il faut multiplier toute la colonne « Abricots » par 2 par rapport à la colonne personnes, donc pour 4 personnes, on devrait avoir 4 x 2 = 8 abricots.
– il faut multiplier toute la ligne « 4 personnes » par 4 par rapport à la ligne « 1 personne », donc pour 4 personnes, on devrait avoir 2 x 4 = 8 abricots.
Repères :
Chaque fois qu’on me donne une relation entre 2 éléments et que je veux calculer d’autres quantités pour ces éléments.
Entraîne-toi :
Tu trouveras des exercices à faire en cliquant ici pour te rendre sur le site Revisez.eu.
![]()
![]()
![]()
