Sujet :
Vocabulaire des opérations : la commutativité
Description :
Savoir et retenir ce que veut dire « la commutativité »
Pré-requis :
- connaître les opérations de base (addition, soustraction, multiplication, division)
- leçon sur « Multiplication : Echanger les nombres ».
Leçon :
Révision
Dans la leçon sur les additions, tu as vu que l’ordre des nombres n’avait pas d’importance. Par exemple :
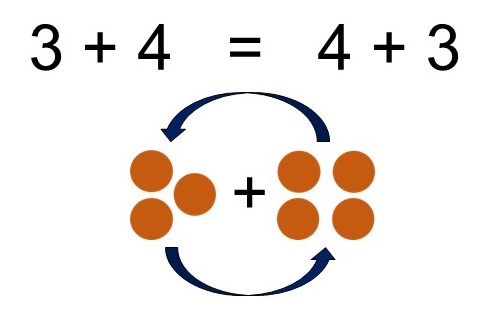
Cette propriété de l’addition, ce fait de pouvoir échanger la place des nombres autour du « + », s’appelle la commutativité.
On n’utilise presque jamais le verbe commuter, mais il veut bien dire « changer ». On peut aussi dire « permuter » les nombres.
Donc, que tu commutes, ou bien changes la place, ou bien permutes les nombres d’une addition, le résultat restera le même.
Définition de la commutativité
« Commutativité : propriété d’une opération qui permet de changer l’ordre des termes sans en changer le résultat. »
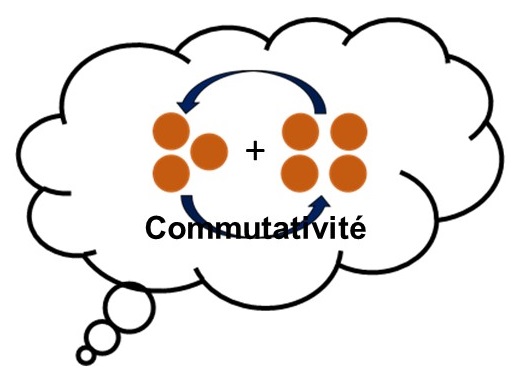
En d’autres termes, une opération est commutative lorsque l’on peut changer les nombres de place sans que cela change le résultat.
Quelles autres opérations possèdent cette même propriété de commutativité ?
Essayons avec la soustraction : si elle était commutative, cela voudrait dire que 4-3 = 3-4. Est-ce que c’est le cas ?
Calculons la partie de gauche : 4 – 3 =1.
Calculons la partie de droite : 3 – 4 . C’est 3 dont j’enlève 4, donc je n’y arrive pas, il me manque 1 pion !
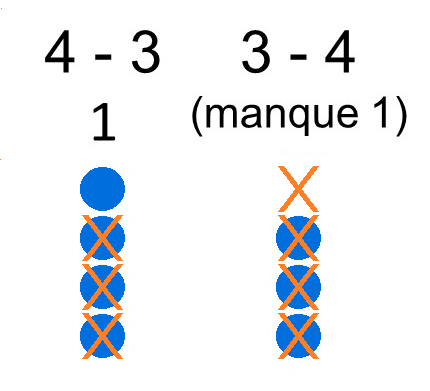
Donc 4-3 et 3-4 ce n’est pas du tout pareil. La soustraction n’est pas commutative !
Essayons avec la multiplication : La multiplication est-elle commutative ?
Dans la leçon « Multiplication : Echanger nombres », tu sais que l’on peut échanger les nombres dans une multiplication.
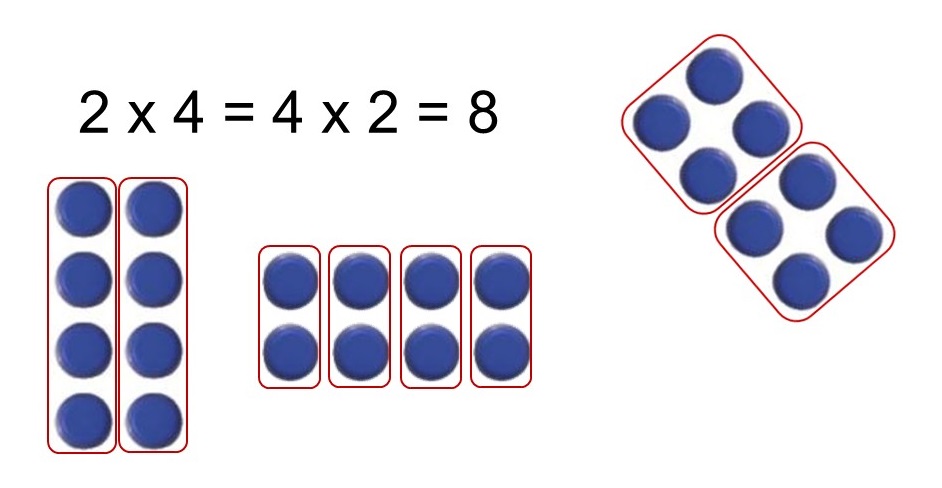
Le résultat est le même. La multiplication est commutative.
Essayons avec la division : Est-ce que 2 : 4 = 4 : 2 ?
2 : 4 c’est égal à… ½, donc 0,5
4 : 2 c’est égal à… 2
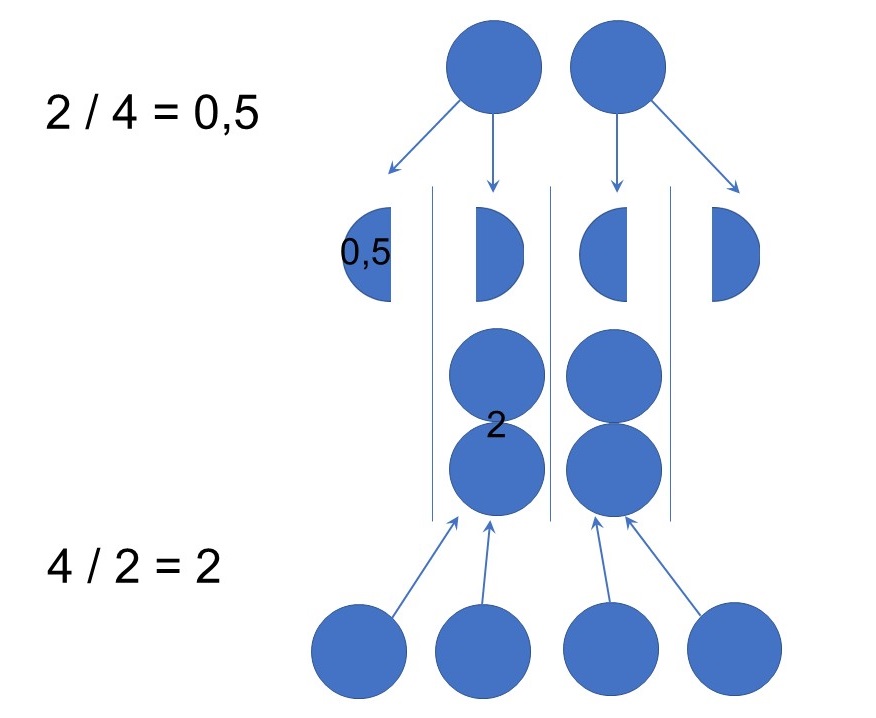
Ce n’est pas pareil du tout. La division n’est pas commutative.
En résumé…
Mémorise bien le récapitulatif suivant.
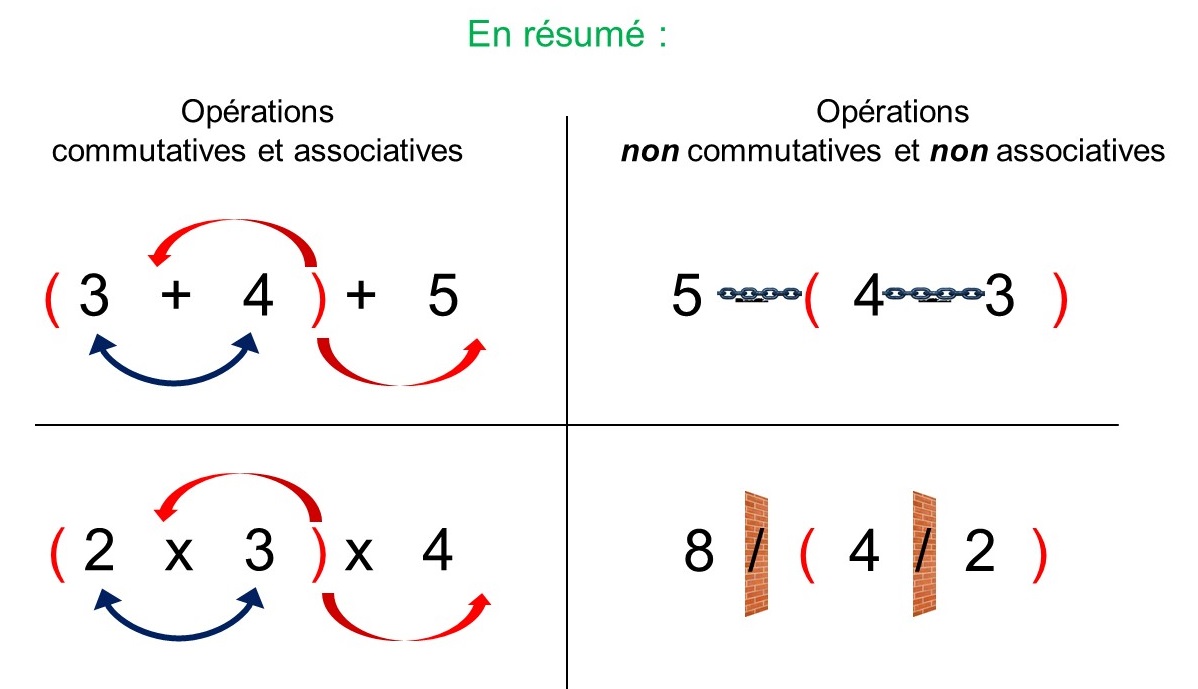
Repères :
Quand je fais une opération, j’utilise le vocabulaire qui convient.
Je regarde si c’est plus pratique de changer l’ordre des termes d’une addition ou d’une multiplication.
Entraîne-toi :
Lorsque tu feras des exercices, vérifie que tu sais donner un nom à tous les nombres et symboles de ton calcul.
Et repère aussi si c’est plus pratique de changer l’ordre des nombres MAIS ATTENTION, SEULEMENT POUR LES ADDITIONS ET LES MULTIPLICATIONS.
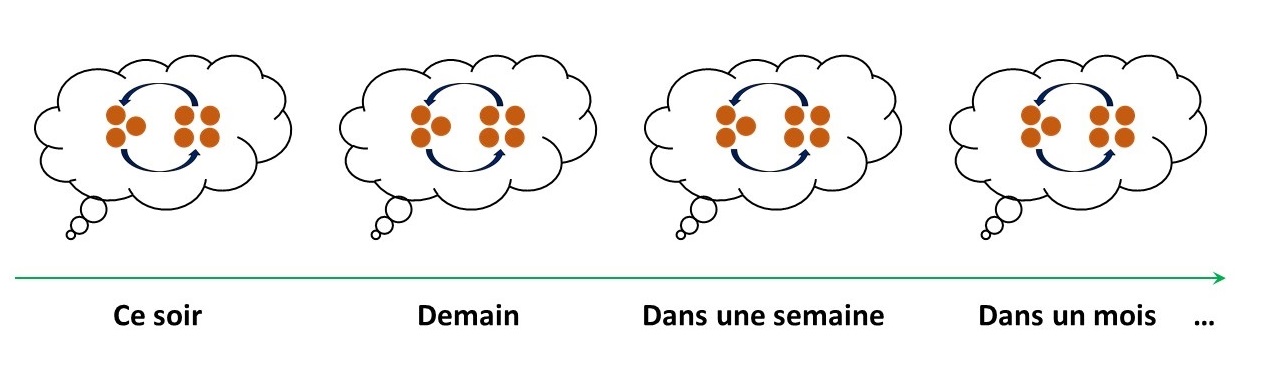
Et pour mémoriser à plus long terme, il faut re-dire souvent à son cerveau que c’est important, qu’il doit s’en souvenir, donc re-voir l’image régulièrement. Il faut re-viser, re-visualiser.
![]()
![]()
![]()
