Sujet :
Fractions & Proportions
Description :
Dans cette leçon nous voyons les 2 cas où l’on peut comparer des fractions de manière immédiate, sans calculs ou transformations intermédiaires.
Leçon :
Prérequis : les leçons « Fractions : initiation » et « Fractions : 2 significations »
Tu te souviens qu’une fraction peut être représentée comme un nombre de petits morceaux, de fragments d’unité. Par exemple 1/5, c’est un cinquième : on coupe une unité en 5 et on prend un morceau.
2/5, c’est 2 cinquièmes : on coupe une unité en 5 et on prend 2 morceaux.
Comparer des fractions de même dénominateur
Pour comparer 2/5 et 3/5, comme je parle des mêmes types de morceaux (des cinquièmes), il me suffit de comparer leur nombre. 2 < 3 donc 2/5 < 3/5 (2 cinquièmes < 3 cinquièmes).
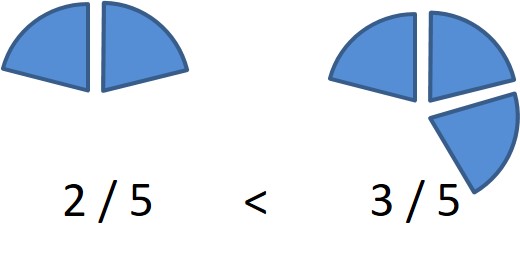
C’est comme si je disais 2 choux < 3 choux.
Mais je ne peux pas comparer des éléments différents, donc je ne peux pas comparer facilement 2/5 et 4/6, car je ne parle pas des mêmes éléments. Il faudrait faire des transformations que tu verras bien plus tard.
Comparer des fractions de même numérateur
Comparons maintenant les éléments :

Que remarques-tu ?
On voit que plus le dénominateur est grand, plus on coupe l’unité, et plus les morceaux sont petits.
Quand le numérateur est le même, il y a le même nombre de morceaux, et il suffit donc de comparer leur taille.
Ex. 3/4 < 3/5
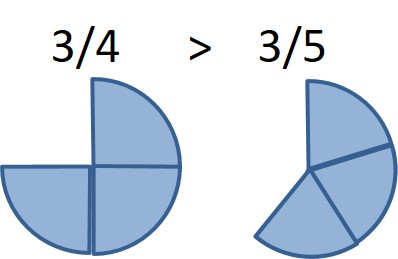
Comme d’habitude, le secret est de bien voir de quoi on parle dans sa tête, et cela devient évident !
Repères :
Quand je dois comparer des fractions, je commence par regarder si je peux comparer le nombre de morceaux et/ou leur taille. Si ce n’est pas le cas, je dois attendre la leçon suivante 😉
